Lesson: Graphs & Heuristics

1. Introduction to Graphs

A graph is a data structure used to represent relationships between objects. A graph consists of:

  • Nodes (Vertices): The entities being connected.
  • Edges: The connections or relationships between nodes.

Graph Example

Types of Graphs

  • Undirected Graphs: Edges are bidirectional (e.g., Facebook friendships).
  • Unweighted Graphs: All edges are considered equal.
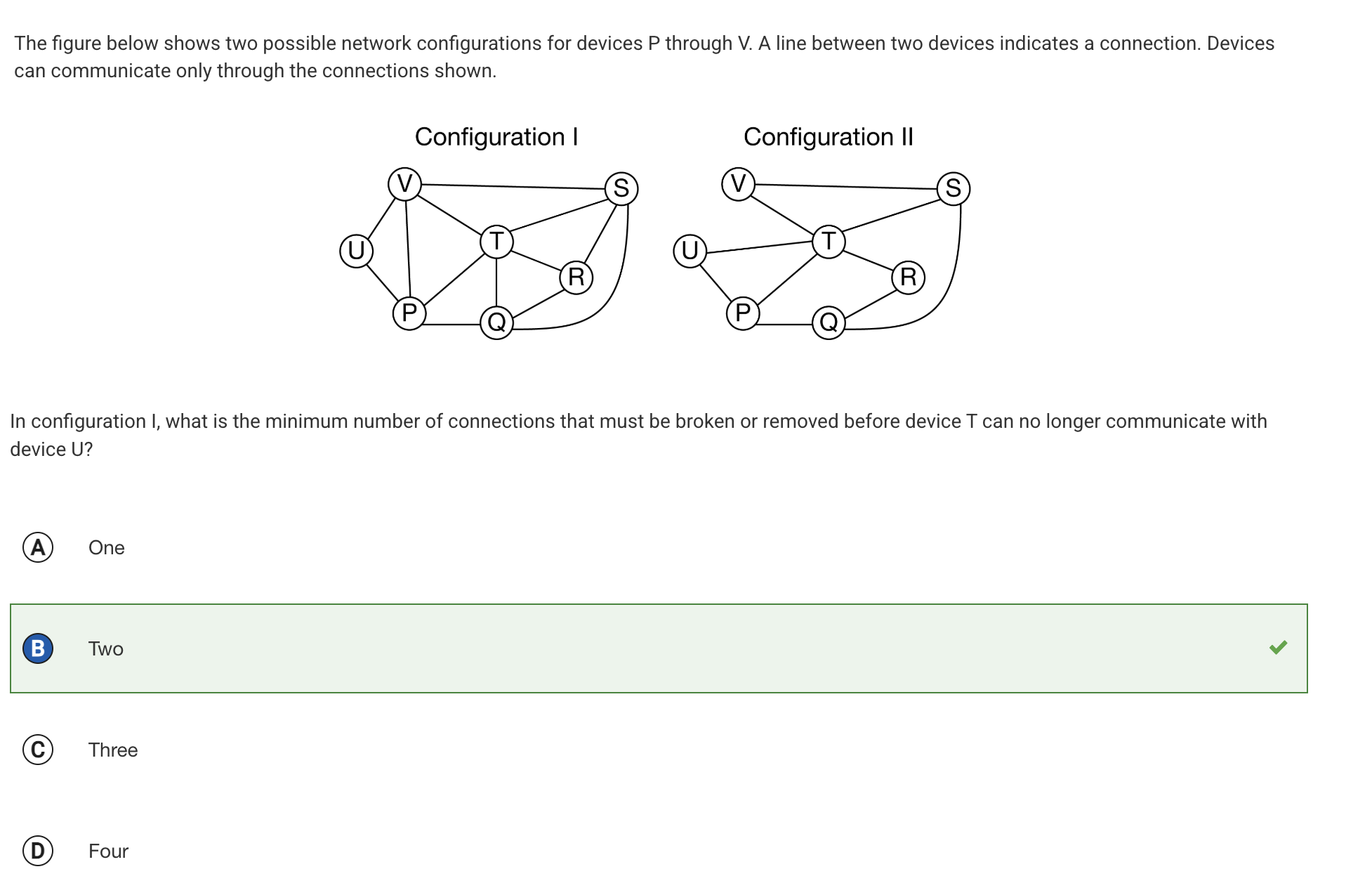
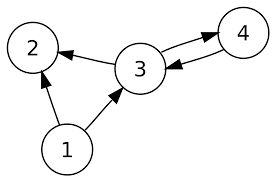
  • Directed Graphs: Edges have direction (e.g., Twitter followers). Directed Graph
  • Weighted Graphs: Edges have values, such as distance or cost (e.g., road networks). Weighted Graph

Applications of Graphs

  • Social Networks: Connecting users and their relationships.

Graph Application

  • Navigation Systems: Finding the shortest route in Google Maps.
  • Recommendation Systems: Netflix suggesting movies based on connections between viewers and genres.

Popcorn Hack #1

True or False: In a directed graph, an edge from node A to node B implies that there is always a corresponding edge from node B to node A.

3. Heuristics

A heuristic is a problem-solving approach that simplifies the solution process by using rules of thumb.

Real-World Example

  • Brute Force Approach: Check every shelf one by one.
  • Heuristic Approach: Go directly to the Science section if you’re looking for a science book.

Examples of Heuristic Algorithms

  • Greedy Algorithms: Always choose the best immediate option.
  • A* Search: Finds the quickest path from one point to another.

Real-World Application of Heuristics

Navigation: In Google Maps, an approximation of the shortest route is calculated using heuristics (Dijkstra’s algorithm).

Popcorn Hack #2

True or False: Heuristics always provide faster solutions than exact algorithms, but they may sacrifice accuracy for speed.

Traveling Salesman Problem (TSP)

The Traveling Salesman Problem (TSP) is a famous optimization problem in computer science and mathematics. It asks:

“Given a set of cities and the distances between them, what is the shortest possible route that visits each city exactly once and returns to the starting point?”

Small Example:

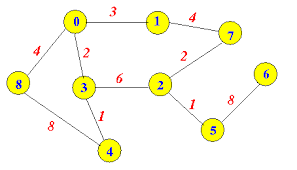
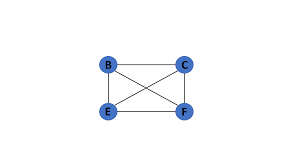
Graph Example

A greedy heuristic like the Nearest Neighbor Algorithm is often used to approximate a solution, but it doesn’t always find the best path.

Large Example:

Graph Example

Why is TSP Hard?

  • With n cities, the number of possible routes is (n-1)!, meaning the number of paths grows exponentially.
  • For large graphs, brute-force checking all routes is too slow, making heuristics and optimization necessary.

Example of Route Growth:

Cities (n) Possible Routes ((n-1)!)
4 6
5 24
10 3,628,800
100 More than the atoms in the universe! 😲💥

Popcorn Hack #3

True or False: While heuristic algorithms like the Nearest Neighbor algorithm can significantly reduce the computational time for TSP, they can never guarantee an optimal solution, and the gap between the heuristic solution and the optimal solution can grow exponentially as the number of cities increases.

Homework:

Explore the concept of “Social Network Analysis” and explain how graphs are used in analyzing social media platforms. Specifically, focus on:

  • How are users (nodes) and relationships (edges) represented in social networks?

  • Provide one example of a real-world social media platform where graph theory plays a crucial role.